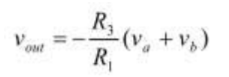4/25 Inverting Differentiator

Today, we introduced an integrator which is an op amp circuit whose output is proportional to the integral of the input signal, and a differentiator which is an op amp circuit whose output is proportional to the rate of change of the input signal.
We derived a equation for the integrator.

Different input voltage will have different output voltage.

Then, we talked about the switching function including step function, impulse function, and ramp function.
The unit step function u(t) is 0 for negative values of t and 1 for positive values of t.


Next, we did lab.

Inverting Differentiator
Pre-lab

The frequency should be 234Hz to get a gain of -1.
The actual resistor we used is 665ohms.

Apply a sinusoidal input voltage with frequency = 100Hz, amplitude = 1V, and offset = 0V to the circuit of Figure 1.

Apply a sinusoidal input voltage with frequency = 250Hz, amplitude = 1V, and offset = 0V to the circuit of Figure 1.

Apply a sinusoidal input voltage with frequency = 500Hz, amplitude = 1V, and offset = 0V to the circuit of Figure 1.

The table below is the comparison of the expected output voltage and the experimental output voltage.

Summary

We learned about integrator and differentiator, and step function, impulse function, and ramp function. By doing the lab, we can see that how differentiator work and how it affects the circuit by looking at the result of the graph and the table. 

4/18 Passive RC Circuit Natural Response & Passive RL Circuit Natural Response

We started with inductors with series and parallel.
It's the same as resistors.
The equivalent inductance of series-connected inductors is the sum of the individual inductances, and the equivalent inductance of parallel inductors is the reciprocal of the sum of the reciprocals of the individual inductances.

Here is the example we did in the class.

The equivalent inductance for this question is 15H.

Next, we talked about first order RC and RL circuits.

A source-free RC circuit occurs when its dc source is suddenly disconnected. The energy already stored in the capacitor is released to the resistors. A circuit response is the manner in which the circuit reacts to an excitation.

(From Day 16 1st Order Circuits.pdf)

There are two important relationships:

Both relations take 5 time constant to reach the final state or the steady state.

We did a example.

Passive RC Circuit Natural Response

Pre-lab

Estimation the time constant for the circuits of Figures 2(a) and 2(b).

For figure 2(a) the 5 time constant = 0.352s, and for figure 2(b) the 5 time constant = 0.0756s

The actual resistance for R1 = 0.977 ohms and R2 = 2.16k ohms.

This is the basic set up for this lab.

Figure 2(a)

We got almost the same value for the 5 time constant. (Forgot to take a picture for the initial time that started to drop)

Measured 5 time constant = 0.343s

Calculated 5 time constant = 0.352s

% error = 2.56%

Figure 2(b)

We got almost the same value for the 5 time constant. (Forgot to take a picture for the initial time that started to drop)

Measured 5 time constant = 0.08158s

Calculated 5 time constant = 0.0756s

% error = 7.91%

Passive RL Circuit Natural Response

Don't have time to do pre-lab

The picture below is the result for figure 2(a)

Summary

We learned how to deal with inductors with series or parallel, RC and RL circuits, and how to determine the time constant in a real world circuit.

Recently, if the class had the second lab at that day, the time would not be enough to finish the second lab. We spent to much time on the first lab. Limiting the time for the first lab would help to solve this problem.

4/13 Capacitor Voltage-current Relations & Inductor Voltage-current Relations

We talked about capacitors and Inductors today.

Capacitor

A capacitor consists of two conducting plates separated by an insulator (or dielectric). (From Day 15 Capacitors and Inductorsb.pdf)

The unit is farads (F).

We started with figuring out the unit of the capacitance. 

C is proportional to area/distance which is the unit m.

In order to get the correct unit, we need to have a constant which is the permittivity of the dielectric material between the plates.

Next, we did a example.

The video is when we apply too much voltage to the capacitor. We exploded a capacitor.

Capacitor Voltage-current Relations

Pre-lab

We predicted that the capacitor voltage and the capacitor current if the capacitor voltage is a sinusoidal wave and a triangular wave.

The picture below is the prediction.

The picture below is the basic set up for this lab.

The actual resistance is 99.2 ohms.

The picture below is when applying a sinusoidal input voltage with frequency = 1kHz, amplitude = 2V, and offset = 0V to the circuit.

The picture below is when applying a sinusoidal input voltage with frequency = 2 kHz, amplitude = 2V, and offset = 0V to the circuit .

The picture below is when applying a triangular input voltage with frequency = 100 Hz, amplitude = 4V, and offset = 0V to the circuit.

Next, we leaned how to deal with the problem that the capacitors are series or parallel. It's the opposite of resistors.

For the example above, the equivalent capacitance would be 20 micro farads.

Inductor

An inductor consists of a coil of conducting wire. (From Day 15 Capacitors and Inductorsb.pdf)

The unit is henrys (H).

We did a example. 

By applying the equation, we got the energy stored in the inductor at t = 1s would be 35.7J.

Then, we did the second lab.

Inductor Voltage-current Relations

The actual resistance is 99.2 ohms.

The picture below is the basic set up for this lab.

The picture below is when applying a sinusoidal input voltage with frequency = 1kHz, amplitude = 2V, and offset = 0V to the circuit.

The picture below is when applying a sinusoidal input voltage with frequency = 2 kHz, amplitude = 2V, and offset = 0V to the circuit.

Summary

We leaned how capacitors and inductors work in the circuits, and how to calculate the equivalent capacitance when the capacitors are in series or parallel, and why we use capacitors and inductors in a circuit. Also, we learned the important equations for calculating the energy stored in the capacitors and the energy stored in the inductors.

4/11 Temperature Measurement System Design & Wheatstone Bridge Circuits

We talked about cascaded op amp circuits.

A cascade connection is a head-to-tail arrangement of two or more op amp circuits such that the output of one is the input of the next.

(From Day 14.5 Cascaded Op Amps2.pdf)

We did a example of cascaded op amp circuit below:

We could see the circuit as two separate circuit and solve it by cutting it half.

 After this example, we did the lab.

Temperature Measurement System Design

In order to have a voltage output greater than 2, we need to find R1 and R2 that satisfy this situation, so we pick R1 to be 10k ohms and R2 to be 56k ohms.

In this lab, there were two parts. One is Wheatstone bridge design, and another is difference amplifier design.

The circuit below was our design of this lab.

The actual values of resistance are next to the resistor symbols.

The picture below is the basic set up for Wheatstone bridge design.

By balancing the bridge, we got the voltage across the thermistor to be 0V at room temperature like the picture shown below.

And this is the video that show the bridge working:

At room temperature, the voltage across the thermistor is 0V, and at body temperature, the voltage across the thermistor is 1.05V.

Next step, we connected Wheatstone bridge to a difference amplifier to produce a voltage output greater than 2V.

The video below shows that the entire system working:

From the video, we could see that the range of voltage output is from 0V to 4.12V, which satisfies the result what we expected the circuit to have.

By designing this circuit, we can make the output voltage whatever we want by easily changing R1 and R2.

After the lab, we leaned Instrumentation Amplifiers, which is the most useful and versatile op amp circuits for precision measurement and process control.

The voltage output follows the equation below:

 

The instrumentation amplifier is an extension of the difference amplifier in that it amplifies the difference between its input signals.

(From Day 14.5 Cascaded Op Amps2.pdf)

Summary

We leaned how to set up a temperature measurement system and how to balance Wheatstone bridge. Also, we learned a new amplifier, called Instrumentation Amplifiers. By learning these amplifiers, we can easily change the original voltage input to any output voltage we want.

4/6 Summing Amplifier & Difference Amplifier

We learned many other amplifiers today.
We started with the unity gain buffer amplifier.

We did a example to calculate the Vo if Vs = 0 in the circuit above.
By using nodal analysis, we got Vo = -1.6364V.

And then, we talked about Non-inverting Amplifier which is an op amp circuit designed to provide a positive voltage gain.
The relationship between Vin and Vout of non-inverting amplifier is:

Next, we talked about Summing Amplifier.
The relationship between Vin and Vout of summing amplifier is:

indicating that the output voltage is the sum of the inputs. 

Then, we did lab.

Summing Amplifier

The picture above is the basic set up for this lab.

In this lab, the relationship between Vin and Vout is:

The actual resistance of R1=6.71k ohms

R2=6.67k ohms

R3=6.73k ohms

We got the following table and graph.

The data matched the equation.

For Va=3V and 5V, Vout is at saturation.

The picture is the calculated data we expected to get, but the maximum Vout we could get is 5V and -5V, so we can only get the Vout up to -3.44V.

After summing amplifier lab, we talked about Difference Amplifier.

The relationship between Vin and Vout is:

the amplifier must have the property that Vo = 0 when  V1 = V2 . This property exists when

so we can get:

Difference Amplifier

The picture above is the basic set up for this lab.

The relationship between the input and output voltages we determined in the class is the picture below.

The actual resistance of R1=9.94k ohms, R2=19.9k ohms, R3=9.98k ohms, and R4=19.7k ohms.

The table above is when we set Vb=1V, and vary Va.

We got the graph below:

From the data we got, it followed the relationship between the input and output voltages we determined in the class. 

For Va=-4V, -2V, 3V and 5V, Vout is at saturation.

After this lab, we ended up with analyzing a circuit below:

 

This is a non-inverting amplifier circuit.

By using nodal analysis, we can get the relationship between VL and VT.

Summary

We learned about Non-inverting Amplifier, Summing Amplifier, and Difference Amplifier today. By doing the lab, we knew how each amplifier works and what are the differences between different amplifiers. Each amplifier works differently in the circuit, and the relationship between the input and output voltages are different, too. Next class we will learn more amplifiers which are called differentiation and integration amplifiers.