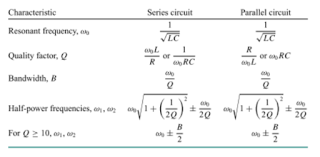
We talked about filters. A filter is a circuit that is designed to pass signals with desired frequencies and reject or attenuate others. (From Day 27 Filters.pdf)
A filter can be used to limit the frequency spectrum of a signal to some
specified band of frequencies.
There are two kinds of filters: passive and active filters.
A filter is a passive filter if it consists of only passive elements R, L, and C.
A filter is an active filter if it consists of active elements (such as transistors and op amps) in addition to passive elements R, L, and C.
The picture shows the differences between four types of filters.

Low pass filter will pass low frequency (C in RC Series or R in RL Series).
High pass filter will pass high frequency (R in RC series).
Band pass filter will pass middle frequency (R in RLC Series).
Band stop filter will pass frequency other than the middle frequency (LC in RLC Series).
We did some example:


Then, we did lab.
Passive RL Filter
Pre-lab

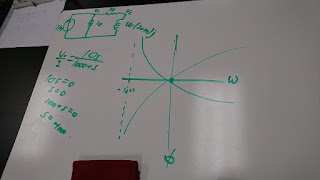
We calculated the cut off frequency, which is 15915Hz.
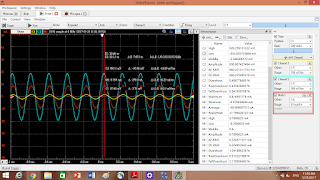
Result:
Before cutoff frequency (Resistor Voltage)




At the cutoff frequency and after:





Before the cutoff voltage:




In and after the cutoff frequency:





The graph below are the the graphs for phase vs frequency and transfer function vs frequency of the voltage output of the resistor.


The graph below are for phase vs frequency and transfer function vs frequency of the voltage output of the inductor.

Summary
Today, we learned the differences between each filters and did a lab of the resistor voltage acting like a low pass filter and the inductor voltage acting like a high pass filter.