5/25 Apparent Power and Power Factor

Today, we talked about effective or RMS value, apparent power, power factor, and complex power.
The effective value of a periodic current is the dc current that delivers the same
average power to a resistor as the periodic current.
The effective value of a periodic signal is its root mean square (RMS) value.

The apparent power (in VA) is the product of the RMS values of voltage and current. 

The power factor is the cosine of the phase difference between voltage and current. It is also the cosine of the angle of the load impedance.

Here is the power summary:

The picture below is the relationship between effective value and max value.

We did some example of how we use the equation to find what we want.

Then, we did lab.

Apparent Power and Power Factor

Pre-lab

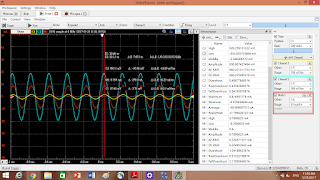
The picture above is when RL=10ohms.

The table below is what we calculated for different resistance value.

The actual resistor we used are 10.8ohms, 47.1 ohms, and 99.3ohms.

The picture below is the basic set up for this lab.

Result:

RL = 10 ohms

The RMS value of load voltage is 627mV.

The RMS value of load current is 18.7mA.

The phase difference is 64.44 degree.

RL = 47 ohms

The RMS value of load voltage is 625.1mV.

The RMS value of load current is 10.68mA.

The phase difference is 36.83 degree.

RL = 100 ohms

The RMS value of load voltage is 660.1mV.

The RMS value of load current is 6.22mA.

The phase difference is 12.6 degree.

The table below is the comparison of experimental value and calculated value.

From the graph above, we successfully verify the apparent power equation Irms*Vrms = Power, and the power factor is cos(V-I).

Summary

Today, we learned many new things: effective or RMS value, apparent power, power factor, and complex power. By learning these terms, we can deal with power in AC circuit, and know how power is viewed in actual world--the importance of power factor in electricity consumption cost.